Simulating Electronic Excitations

Electronic excited states are ubiquitous in all forms of light driven chemistry, but are quite challenging to simulate. Time-dependent density functional theory (TDDFT) is popular for modeling excitations, but is known to fail catastrophically in many regimes. Some chemically relevant examples are charge-transfer states, and excited state bond dissociations (as we recently showed). A large part of my research has focused on developing accurate (and computationally affordable) methods for simulating electronic excitations. The resulting publications can be found here.

Comparison of TDDFT with spin-unrestricted orbitals and exact quantum mechanics for triplet states of dissociating H2. TDDFT potential energy surfaces have derivative discontinuities after the ground state spin-symmetry is broken.

Excited State Orbital Optimization

Excited state models can be improved by optimizing orbitals for individual excited states, instead of just recycling ground state orbitals. This is a challenging task, as excited states are normally unstable stationary points (“saddle points”) of energy. Traditional orbital optimizers thus tend to slip from desired excited state solutions to minima like the ground state instead. We have developed a solution to this “variational collapse” problem. Instead of direct energy extremization, we change the optimization objective to be minimization of the square of the energy gradient. This Square Gradient Minimization (SGM) technique can reliably converge energy saddle points for any electronic structure method. SGM is also relatively cheap, costing only 2-3 times as much as ground state orbital optimization.

Optimizing the 2p to 3p excitation for a single Boron atom with SGM. Traditional ground state solvers like DIIS and GDM instead undergo variational collapse down to the ground state.

Orbital Optimized Density Functional Theory

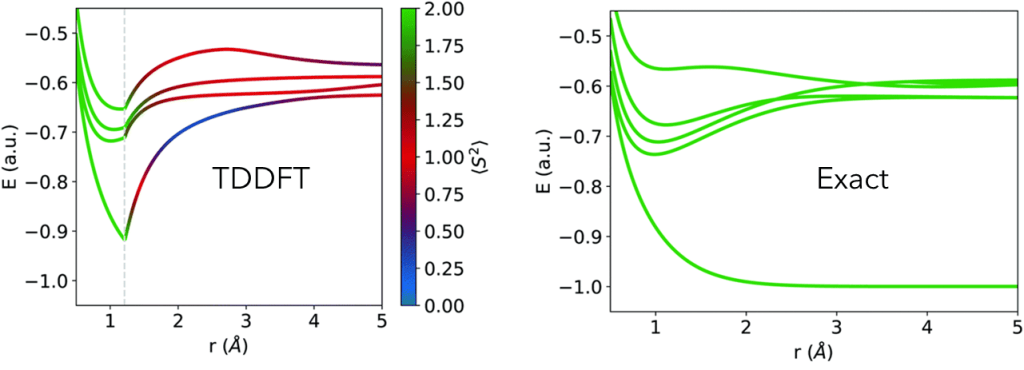
Another challenge in modeling excited states is the presence of unpaired electrons. The wavefunctions for low spin states thus necessarily have significant contributions from multiple Slater determinants. This is nontrivial to model with DFT, as the Kohn-Sham formalism is single determinant by construction. We developed routes to couple arbitrary numbers of unpaired electrons for modeling multideterminant states within KS-DFT. These recoupling techniques, together with excited state orbital optimization, permit the simulation of excited states with Orbital-Optimized DFT (OO-DFT). OO-DFT is accurate for many kinds of electronic excitations traditionally considered to be challenging, as detailed in our perspective article.

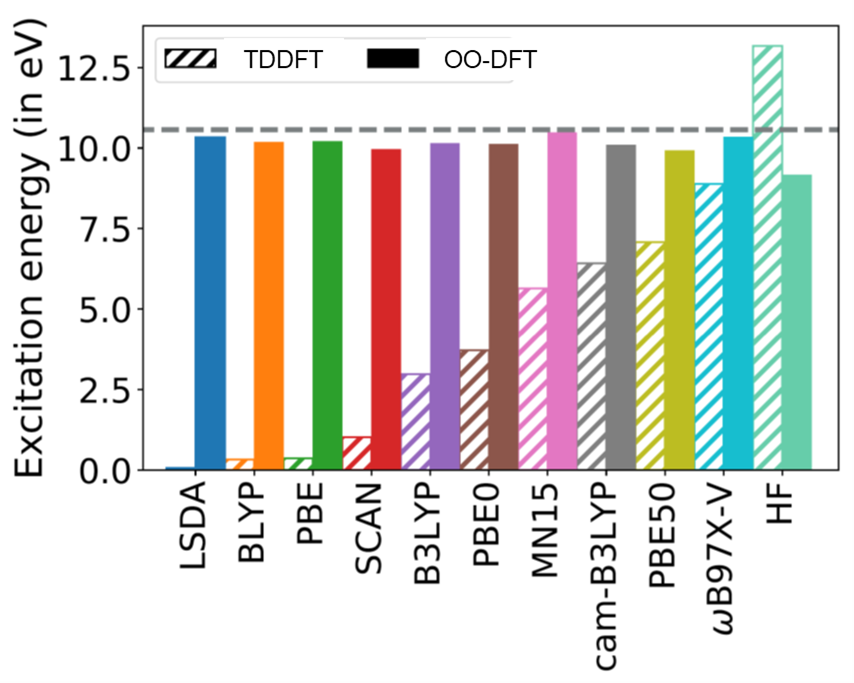
For example, OO-DFT can easily simulate doubly excited states (absent in TDDFT).

Errors in OO-DFT excitation energies vs theoretical best estimates for representative doubly excited states. OO-DFT errors are smaller than those resulting from CC3 (an expensive linear-response coupled cluster approach).

OO-DFT can also simulate charge-transfer well, sans the strong functional dependence seen in TDDFT.

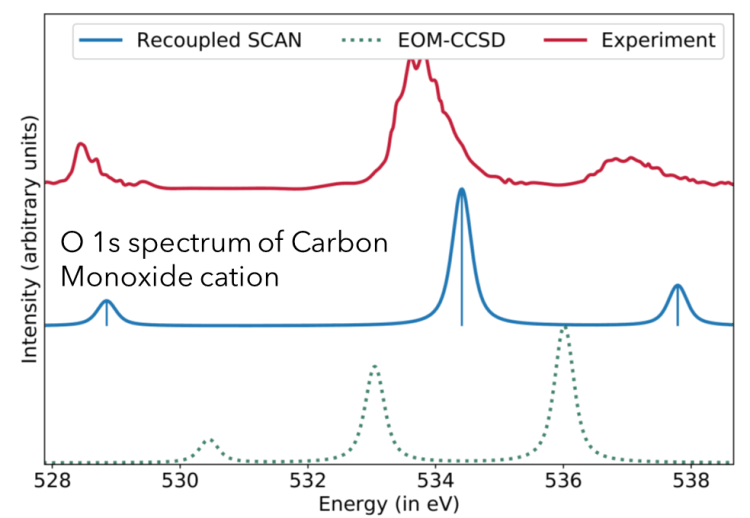
Excitation energy for charge-transfer between infinitely separated ammonia and fluorine, from OO-DFT and TDDFT. The results are compared to a CCSD(T) benchmark (dashed gray line).

Core-level Spectroscopy

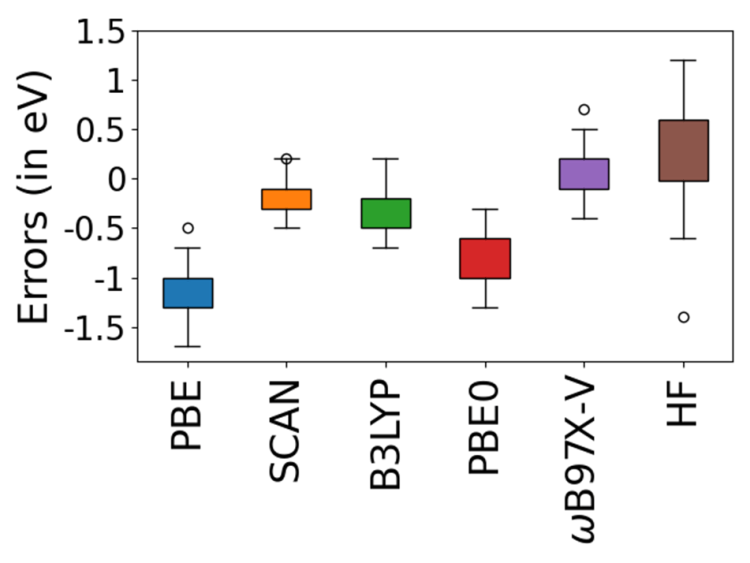
An extremely useful application of OO-DFT is semiquantitative simulation of inner-shell spectra. TDDFT has significant (10-20 eV) errors for X-ray absorption energies, as compared to experiment. Smaller, but perceptible (1-2 eV) overestimation is obtained from coupled cluster methods like EOM-CCSD. In contrast, OO-DFT with the SCAN functional yields semiquantitative accuracy for core-level excitation energies (~0.2 eV RMSE, as compared to 0.1 eV experimental uncertainty). This level of performance is consistently obtained for both closed- and open-shell systems. As a result, computed OO-DFT spectra can be directly compared to experiment, without need for empirical alignment shifts.

Distribution of errors in 1s excitation energies of main-group molecules with OO-DFT with different functionals.
Comparison between SCAN/OO-DFT with recoupling of unpaired electrons, EOM-CCSD and experiment.

We have recently also ventured into relativistic quantum chemistry with OO-DFT, for simulating inner-shell spectra of heavier elements. Nuclear quantum effects in X-ray spectra are also being studied, with OO-DFT yielding more robust behavior than TDDFT/EOM-CCSD for biradicaloid molecules.

The accuracy and computational efficiency of OO-DFT indicates promise in simulation of time-resolved X-ray absorption spectra. I have therefore collaborated with spectroscopists in the groups of Prof. Stephen Leone, Prof. Daniel Neumark, and Dr. Oliver Gessner to study ultrafast photoinduced processes and associated inner-shell spectra (as detailed here).